

The range is the maximum value - minimum value. You take those five measurement results and calculate a range. At the start of each hour, you collect five samples from the production line and measure a quality characteristic, X. The Xbar chart examines the variation between subgroups Suppose you are making a product.The range chart examines the variation within a subgroup.Xbar-R Control Chart Example: Small Average Range Ĭlassical Xbar-R Control Charts The classical Xbar-R control chart is designed to look at two types of variation:.We will then look at how to handle these types of situations by using three control charts. You will see that the control limits on the Xbar chart are very tight and most of the points on that chart are beyond the control limits. We then take a look at what the Xbar-R control charts often looks like when you have situation where there is a significant difference between the within-subgroup variation the between-subgroup variation. We start with a brief review of Xbar-R charts. But what happens when the process is such that is not possible for the short-term variation to be consistent with the long-term variation? This month's newsletter takes a look at how to address situations with control charts where the within-subgroup variation is significantly different from the between-subgroup variation. The long-term variation is given by the between subgroup variation on the Xbar chart. If you are using an Xbar-R chart, the short-term variation is given by the within-subgroup variation on the range chart. But it also means that the short-term variation is consistent with long-term variation. What does it mean when a control chart indicates that a process is in statistical control? It means it is consistent and predictable - you can predict what the process will do in the near future. In a mixture pattern, the points tend to fall away from the center line and instead fall near the control limits.Xbar-mR-R (Between/Within) Control Chart January 2011 Control charts are really a study in variation. Test 8: Eight points in a row more than 1σ from center line (either side) Test 8 detects a mixture pattern. Control limits that are too wide are often caused by stratified data, which occur when a systematic source of variation is present within each subgroup. This test detects control limits that are too wide. Test 7: Fifteen points in a row within 1σ of center line (either side) Test 7 detects a pattern of variation that is sometimes mistaken as evidence of good control. Test 6: Four out of five points more than 1σ from center line (same side) Test 6 detects small shifts in the process. Test 5: Two out of three points more than 2σ from the center line (same side) Test 5 detects small shifts in the process. You want the pattern of variation in a process to be random, but a point that fails Test 4 might indicate that the pattern of variation is predictable. Test 4: Fourteen points in a row, alternating up and down Test 4 detects systematic variation. This test looks for a long series of consecutive points that consistently increase in value or decrease in value. Test 3: Six points in a row, all increasing or all decreasing Test 3 detects trends.
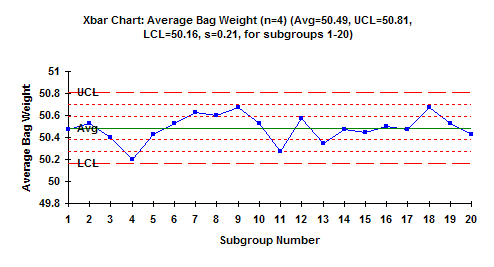
If small shifts in the process are of interest, you can use Test 2 to supplement Test 1 in order to create a control chart that has greater sensitivity. Test 2: Nine points in a row on the same side of the center line Test 2 identifies shifts in the process centering or variation. Test 1 is universally recognized as necessary for detecting out-of-control situations. Test 1: One point more than 3σ from center line Test 1 identifies subgroups that are unusual compared to other subgroups. Only Tests 1−4 apply to the R chart portion of this control chart. Test 2 detects a possible shift in the process.Įight tests are available with this control chart. For example, Test 1 detects a single out-of-control point. Each of the tests for special causes detects a specific pattern or trend in your data, which reveals a different aspect of process instability. Use the tests for special causes to determine which observations you may need to investigate and to identify specific patterns and trends in your data.


 0 kommentar(er)
0 kommentar(er)
